Regular Expressions
What are regular expressions?
Regular expressions (REs) are notations for describing sets of character strings. They are used in search engines, text editors, and other tools to search for patterns in text. This concept falls under Type III languages in the Chomsky hierarchy.
A matched string is a set of characters described by a certain arbitrary regular expression. The simplest regular expression is a single literal character like $a$ or $b$. However, not all literals are regular expressions; there are exceptions like $+$, $?$ and . which are called meta-characters. They are used as operators in the expression of the RE language. They can be escaped using characters like \ (backlash), which itself is a meta-character.
Two regular expressions can be alternated or concatenated to form a new regular expression.
For example:
- If the expression $e_1$ matches set $S$ and expression $e_2$ matches set $T$, then $e_1|e_2$ matches union of sets $S \cup T$. This is called alternation.
- The expression $e_1e_2$ matches the concatenation $ST$, this is called concatenation.
Repetition Operators
- $e_1^*$ matches 0 or more occurrences of $e_1$ (Kleene Star).
- $e_1^+$ matches 1 or more occurrences of $e_1$.
- $e_1^?$ matches 0 or 1 occurrence of $e_1$.
The operator precedence, from weakest to strongest, is:
- Alternation ($|$)
- Concatenation
- Repetition operators ($*$, $+$, $?$)
Parentheses can be used to force different meanings. For example, $ab|cd$ is interpreted as $(ab)|(cd)$, whereas $a(b|c)d$ is distinct. Similarly, $ab^$ is equivalent to $a(b^)$.
Note: The above is the traditional syntax. Extensions like Perl (PCRE) added more operators for conciseness, but sometimes at the cost of performance strings or complexity (e.g., backreferences like (dog|cat)\1 matching dogdog or catcat).
Finite Automata
Finite Automata (FA) can also be used to describe a set of character strings, just like regular expressions. For example, to describe the pattern $a(bb)^*a$, a finite state machine can be used.
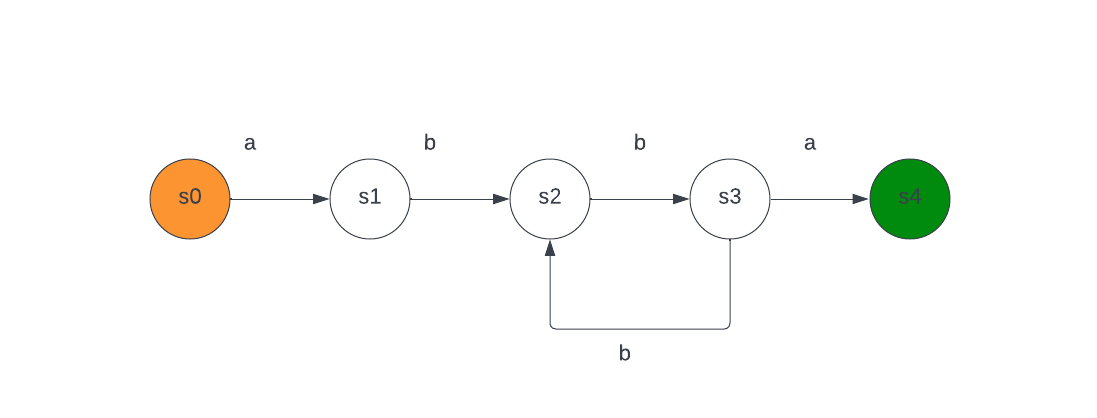
Where $S = {s_0, …, s_4}$ are the states, with $s_0$ being the start state and $s_4$ the matching (accepting) state.
Given a string like abbbba as the input, the machine will transition through states starting from $s_0$. At each stage, the input character “propels” the machine to the next state. If the machine halts in an accepting state after consuming the input, it’s a match. If at any state the input doesn’t have a valid transition, it halts and rejects.
Deterministic vs. Non-Deterministic
The state machine described above is a Deterministic Finite Automaton (DFA). It is deterministic because at any given state, an input symbol leads to at most one new state.
Machines that can choose between multiple states to transition into for the same input are Non-Deterministic Finite Automata (NFA).
The previous diagram could be converted to an NFA. For example:
1 a b b a
2s0 ------> s1 -------> s2 -------> s3 ------> s4
3 | ^
4 |___________|
5 b
If the machine is in state $s_2$ and sees a $b$, it could potentially transition to multiple states in an NFA (if designed that way) or make “epsilon transitions” (transitions without input).
Epsilon Transitions ($\epsilon$): Sometimes it’s useful for NFAs to have “unlabelled” paths (consuming no input).
1 a b b a
2s0 ------> s1 -------> s2 -------> s3 ------> s4
3 | ^
4 |___________|
5 <eps>
This concisely describes $a(bb)^*a$.
Converting RE to NFA
Regular Expressions and NFAs have the same expressive power. We can construct an NFA for any Regular Expression (Thompson’s Construction).
1. Single Character
For a character $a$: $$ s_0 \xrightarrow{a} s_1 $$
2. Concatenation ($e_1 e_2$)
$$ s_0 \xrightarrow{e_1} s_1 \xrightarrow{e_2} s_2 $$
3. Alternation ($e_1 | e_2$)
$$ \begin{align} & \nearrow \xrightarrow{e_1} \searrow \ s_{start} & & s_{end} \ & \searrow \xrightarrow{e_2} \nearrow \end{align} $$ (Glueing the start and end states with $\epsilon$-transitions).
4. Repetition ($e^*$)
This involves adding $\epsilon$-transitions looping back from the end of $e$ to the start, and from the start to the end (to match 0 times).
The process of converting REs to NFAs was formally described by Ken Thompson.
Regular Expression Search Algorithms
To test whether a Regular Expression matches a string:
- Convert the RE to an NFA.
- Run the string on the NFA.
If you end up in an accepting set of states, the RE matches the string. Since NFAs are non-deterministic, running them usually implies keeping track of a set of possible current states at each step.